اطلاعیه شماره ی2
به اطلاع خوانندگان عزیز وارجمند می رساند سعی شده تمام اطلاعات این وبلاگ از مکان های معتبر تهیه وتنظیم ودر اختیار شما عزیزان قرارگرفته باشد تا شما بتوانید باخیالی آسوده از آن ها استفاده کنید.
اما اگر در این وبلاگ در قسمت خاصی از آن اطلاعاتی می بینید که از نظرتان صحیح به نظر نمی رسد لطفا مارا در درستی آن یاری کنید .این وبلاگ در رابطه با بعضی از اطلاعات علمی مسئولیتی قبول نمی کندهر چند این اطلاعات از زیر صافی کارشناسان ماهم رد شد باشد.
فیبو ناچی
توسعه هندسی این دنباله یا سری از اعداد :

این مستطیل را ، مستطیل فیبوناچی نیز مینامند .
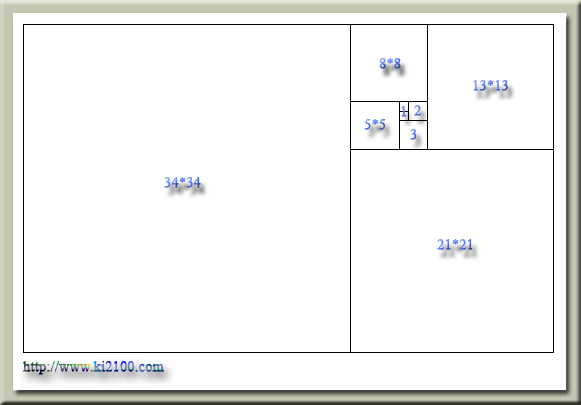
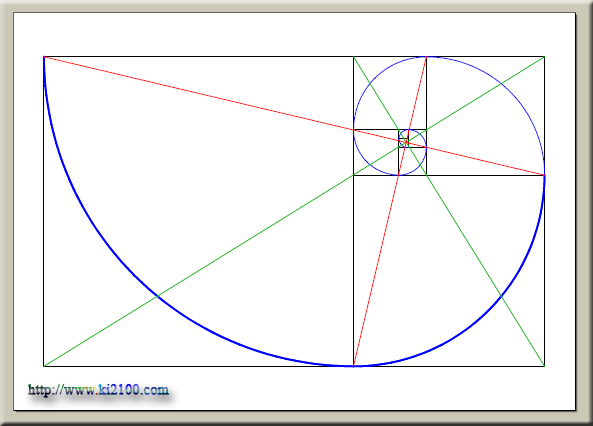
برای رسم مارپیچ طلایی یا فیبوناچی از راس ( گوشه ) هر مربع یک کمان به شعاعی برابر ضلع آن مربع رسم میکنیم . به این مارپیچ بدست آمده ، اسپیرال لگاریتمی هم گفته میشود .
Autodesk DWF format
Adobe Reader PDF format
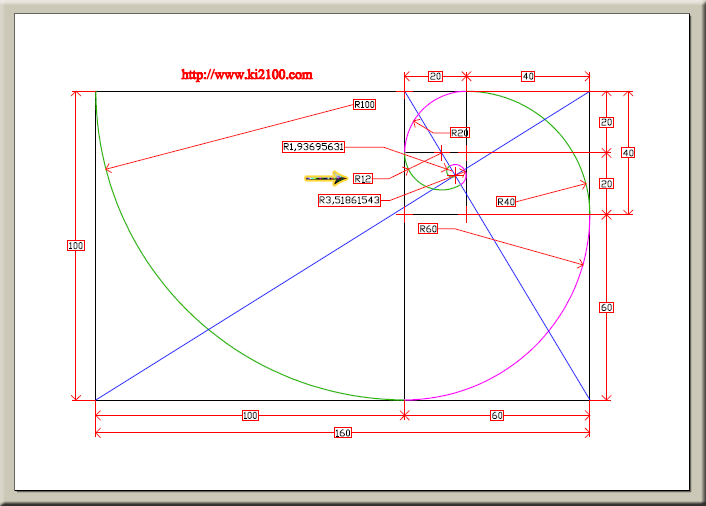
در رسم فوق دنباله را از عدد 20 شروع کردهایم یعنی سری اعداد 20،20،40،60،100 ، در واقع نسبت عرض مستطیل به طول آن را 1.6/1 در نظر گرفتهایم . رسم فوق توسط نرمافزار اتوکد رسم و با دقت 100.000.000/1 اندازه گذاری شده است و طریقه رسم به حد کافی واضح و روشن میباشد و نکته جالب توجه اینکه برای رسم مارپیچ به این روش ، میبایست هفت کمان رسم شود که عدد صحیح 12 برای شعاع کمان پنجم بدست میآید . مرکز هر کمان با علامت جمع مشخص شده است .

Autodesk DWF format
Adobe Reader PDF format
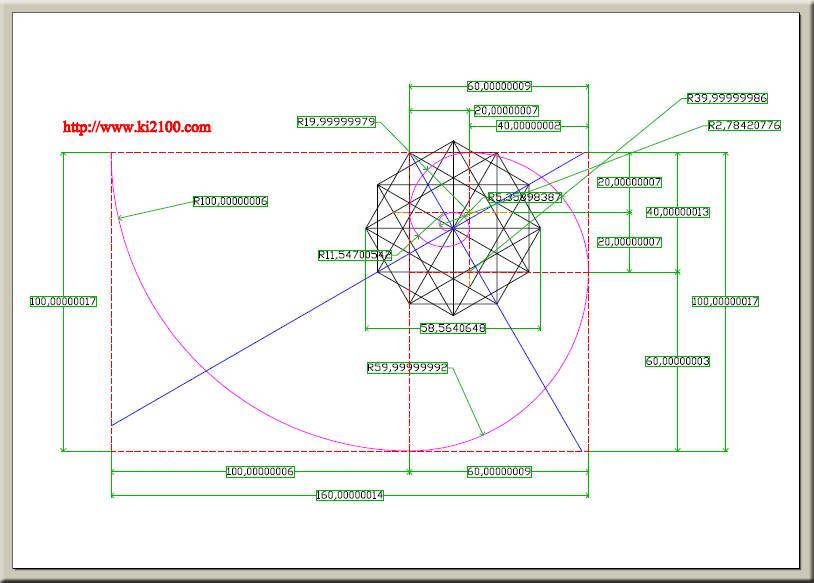
بهطور خلاصه با در نظر گرفتن تقاطعهایی که خطوط با زاویه قائمه یکدیگر را قطع کردهاند ، میتوان مستطیل و مارپیچ طلایی فیبوناچی را در رسم توسعه یافته ستاره داوود رسم نمود . همانطور که مشخص است اختلاف بسیار جزیی این رسم با رسم قبلی مشاهده میشود آنهم در کمانهای 5 ، 6 ، 7 به علت تغییر جزیی در قطرهای آبی رنگ و در تناسبات هندسی اختلافی وجود ندارد ، که دال بر این موضوع است که تناسب طلایی در رسم ستاره داوود توسعه یافته جاری میباشد و در مباحث بعدی توضیح خواهیم داد که کلیه موجوداتی که در آنها تناسبات طلایی دیده میشود ، تناسب خود را مدیون این ترسیمها و ساختارهای هندسی در ستاره داوود توسعه یافته هستند .
Autodesk DWF format
Adobe Reader PDF format
در رسم فوق مستطیل و مارپیچ طلایی به مرکز رسم ستاره داوود توسعه یافته انتقال داده شده است .

Autodesk DWF format
Adobe Reader PDF format
در رسم فوق مستطیل و مارپیچ طلایی به نقطه دیگری انتقال داده شده است .
اینک اگر در این دنباله ( 1,1,2,3,5,8,13,21,34,55,89,144,233 ) هر عدد را به عدد قبلیاش تقسیم کنیم یک چنین سری را بدست میآوریم :
1/1=1 ، 2/1=2 ، 3/2=1.5 ، 5/3=1.66... ، 8/5=1.6 ، 13/8=1.625 ، ....... ، 233/144=1.61805......
که هر چقدر جلوتر برویم بهنظر میآید که به یک عدد مخصوص میرسیم . این عدد را عدد طلایی مینامند که این عدد تقریبا برابر است با :
1.618033................
روش جبری برای بدست آوردن عدد طلایی :
مستطیلی به عرض 1 واحد و طول x را در نظر میگیریم مسلما x بزرگتر از 1 میباشد .
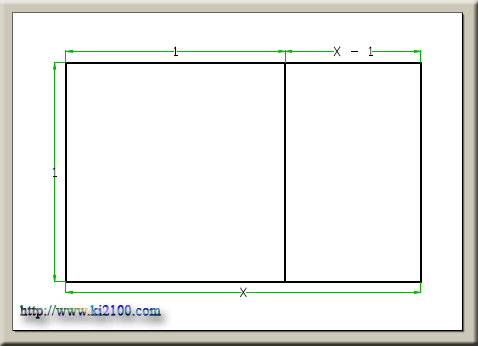
اینک باید مقدار x را چنان تعیین کنیم ( بدست آوریم ) که اگر مربعی به ضلع 1 واحد را از این مستطیل جدا نماییم ، مستطیل بدست آمده کوچکتر ، متناسب مستطیل بزرگتر قبلی باشد ، یعنی x/1=1/(x-1) a به بیان سادهتر ، نسبت طول به عرض مستطیل اول برابر نسبت طول به عرض مستطیل بدست آمده ( مستطیل دوم ) باشد که با ضرب صورت در مخرج طرفین تناسب ، یک معادله درجه 2 بدست میآید یعنی x²-x-1=0 و با ریشهیابی این معادله به ریشههای 1.6180 و 0.6180- دست مییابیم .
روشهای هندسی برای بدست آوردن عدد طلایی :
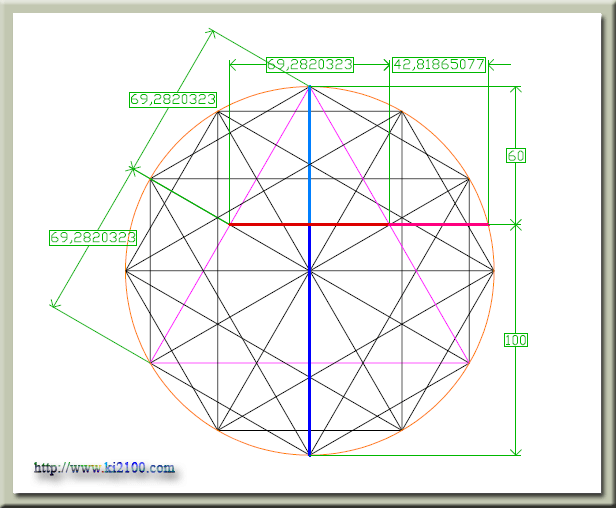
اگر یک مثلث متساویالاضلاع رسم کنیم ( مثلث بنفش ) و از مرکز آن دایرهای رسم کنیم تا از سه راس آن مثلث عبور کند ( دایره نارنجی ) و وسط دو ضلع مثلث را یافته و پاره خطی از آن دو نقطه تا محیط دایره ، رسم کنیم دو پاره خط با نسبت طلایی بدست میآید ( پاره خط زرشکی و سرخ آبی ) یعنی
69.2820323/42.81865077=1.61803398...........
رسم زیر روش دیگری برای رسم مستطیل طلایی ویژه و تناسبات طلایی ، و همچنین بدست آوردن عدد طلایی را نشان میدهد .
Autodesk DWF format
Adobe Reader PDF format
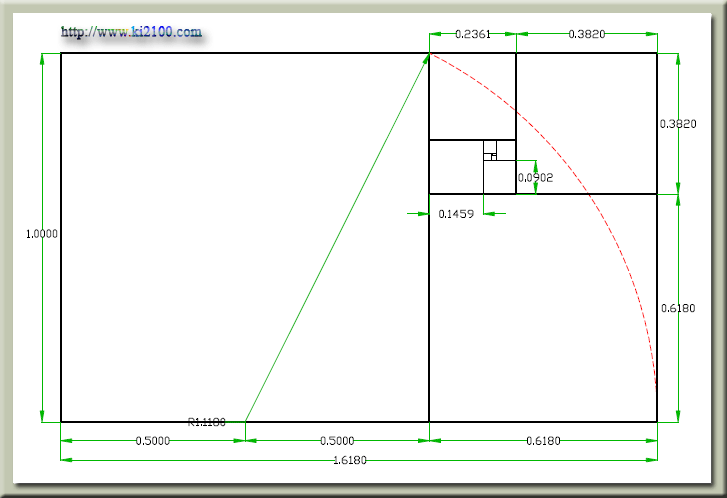
جهت رسم یک مستطیل طلایی به نسبت عدد طلایی ابتدا یک مربع به ضلع یک واحد کشیده سپس طبق شکل فوق وسط ضلع پایینی این مربع را پیدا میکنیم . سپس یک قوس با شعاعی به اندازه وسط ضلع پایینی مربع تا گوشه سمت راست بالا میکشیم تا طول مستطیل معلوم شود .
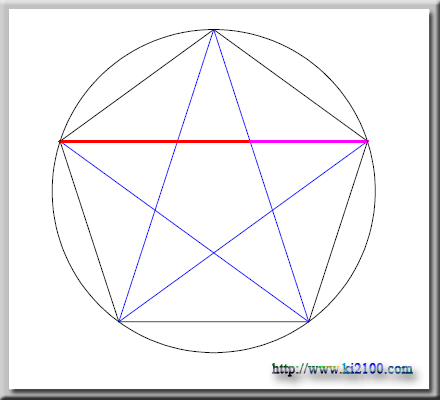
در رسم فوق یک دایره را به پنج قسمت مساوی تقسیم میکنیم . اگر این نقاط را به نقاط مجاور خود وصل کنیم ، مسلما یک پنج ضلعی منتظم خواهیم داشت . اینک اگر نقاط را دو به دو به هم متصل کنیم یک ستاره پنج پر که در داخل آن یک پنج ضلعی منتظم دیگر قرار دارد ، حاصل میشود . در این وضعیت پاره خط قرمز به همراه پاره خط بنفش یک تناسب طلایی را نشان میدهند و به این دلیل مهم ستاره پنج پر برای چشم بیننده ، شکل هندسی خوشآیند و جذابی است که بیانگر این موضوع میباشد که نسبت طلایی در سایر سیستمهای شمارش اعداد نیز آشکار میشود و این ساختار مربوط به اعداد مرموز ( 2 ، 4 ، 6 ) میشود .
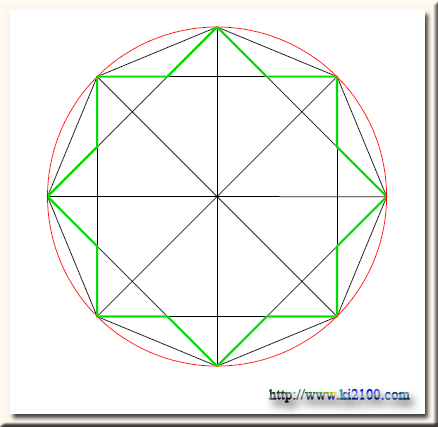
در رسم فوق یک دایره را به هشت قسمت مساوی تقسیم میکنیم . اگر این نقاط را به نقاط مجاور خود وصل کنیم ، مسلما یک هشت ضلعی منتظم خواهیم داشت . اینک اگر نقاط را دو به دو ، چهار به چهار و شش به شش به هم متصل کنیم دو مربع تو در تو حاصل میشود . رسم سبز رنگ مربوط به معماری و هنرهای اسلامی میشود .
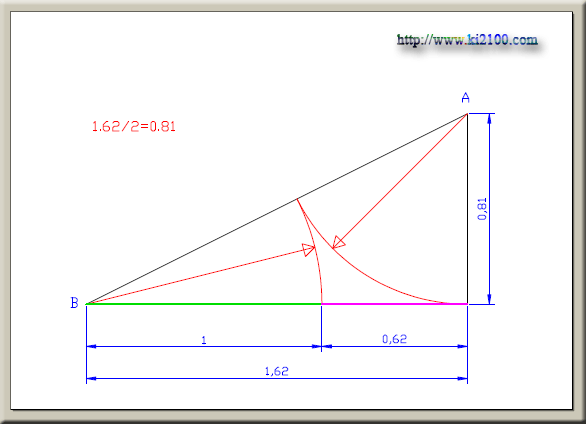
رسم فوق طریقه دیگری برای پیدا کردن ترکیب تناسب طلایی است . به طور مختصر مثلث قائمالزاویهای را رسم میکنیم که طول ضلع افقی آن دو برابر ضلع عمودی باشد . کمان اول را به شعاع ضلع عمودی از مرکز A رسم میکنیم تا وتر مثلث را قطع کند . سپس از محل تقاطع ، کمانی به مرکز B رسم کرده تا ضلع افقی را قطع کند . دو پاره خط سبز و بنفش رنگ ترکیب تناسب طلایی را مشخص میکنند .
اهرام :
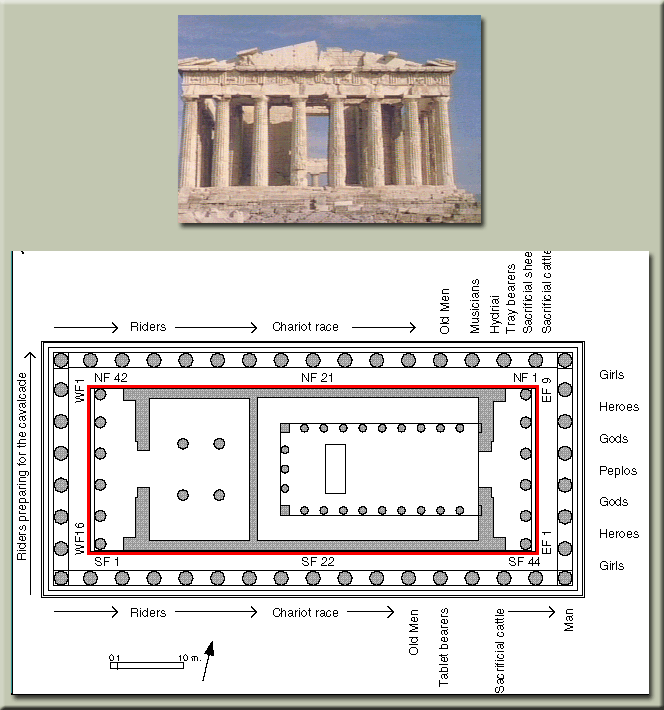
جالب است بدانیم که نسبت ضلع بلندتر به ضلع کوتاهتر مستطیل طلایی که نسبت طلایی نامیده میشود ، در بسیاری از طرحهای هنری از قبیل معماری و خطاطی ظاهر میشود . مطابق تحقیقات انجام شده ، نسبت طول ضلع قاعده به ارتفاع در اهرام ثلاثه مصر ، برابر نسبت طلایی است . همچنین دیوارهای معبد پارتنون از مستطیلهای طلایی ساخته شده است ! زیرا به اعتقاد سازندگان آنها ، مستطیلها با نسبتهای طلایی به چشم خوشایندتر هستند و این موضوع دال بر این واقعیت است که این تناسبات هندسی در ذات انسانها نیز شکل گرفتهاند !

تعریف ریاضی سری اعداد یا دنباله فیبوناچی و عدد طلایی ( فی Φ ) :
غیر از دو عدد اول ( 0 و 1 ) اعداد بعدی از جمع دو عدد قبلی خود بدست میآیند . اولین اعداد این سری عبارتند از :
۰,۱,۱,۲,۳,۵,۸,۱۳,۲۱,۳۴,۵۵,۸۹,۱۴۴,۲۳۳,۳۷۷,۶۱۰,۹۸۷,۱۵۹۷,۲۵۸۴,۴۱۸۱,۶۷۶۵,۱۰۹۴۶
این سری از اعداد به نام لئوناردو فیبوناچی ریاضیدان ایتالیایی نام گذاری شده است . طبق تعریف :
![]()
مقدار عددی حد فوق به عدد فی یا همان .......... 1.618033 میرسد . اگر عدد فی را بتوان دو برسانیم مثل این است که یک واحد به عدد فی افزوده باشیم یعنی Φ²=Φ+1 و اگر عدد یک را بر فی تقسیم کنیم مثل این است که یک واحد از عدد فی کم کرده باشیم یعنی :
1/Φ=Φ-1
عدد فی را در مبنای دوجینی میتوان به صورت 1.75 نوشت که مقدار واقعی ، حقیقی و درستی جهت فی میباشد برای اینکه :
1+(7/12)+(5/12/12)=1.618055555555555555555..........
233/144=1.618055555555555555......
همانطور که میدانیم عدد 233 توالی دوازدهم سری یا دنباله فیبوناچی است یعنی همان تعداد خرگوشها در پایان ماه دوازدهم . و بدست آمدن عدد 1.75 در مبنای دوجینی برای مقدار فی بیانگر این موضوع است که سیستم دوجینی از بعضی جهات راحتتر از سیستم دهدهی است . راحتی فوق اصولا از این حقیقت ناشی میشود که تعداد مقسوم علیههای دوازده از تعداد مقسوم علیههای ده بیشتر میباشد . دوازده بر یک ، دو ، سه ، چهار ، شش و خودش بخشپذیر است . بنابراین بسیاری از محاسبات دستی در سیستم دوجینی تا حدودی سادهتر از سیستم دهدهی هستند ، عدد فی که در مبنای دهدهی به صورت عددهای کسری متناوب در میآید در مبنای دوجینی چنین نیست و میتوان به مقدار فیکس شده 1.75 دست یافت .
مایاهایی که در خلال سالهای 2000 تا 900 قبل از میلاد ، ساکن آمریکای جنوبی بودهاند ، چنین به نظر میرسد که برای رصد کردن حرکات متغیر اجرام آسمانی ، اهرامی بنا نهادند و تقویم شمسی دقیقی وضع کردند . همچنین با محاسبات خود ، وقوع خسوف و کسوف را پیش بینی و مراسم قربانی کردن انسانها را تدارک میدیدهاند و عقیده بر این داشتند که این کار آنها خشم خدایان را از آنها برطرف میکند .

به یقین میتوان گفت که مطالب و موضوعات بسیار مهمی در علوم بشریت در زمینه ریاضیات ، هندسه و نجوم مفقود و از بین رفته است و فقط نشانههای تلخ و ناخوشایندی از آن دانستهها در ساختههای دست بشر باقیمانده است که در مباحث بعدی سعی خواهیم کرد این دانستههای از بین رفته را بازیابی نماییم . البته ما باید مابین علم و جنایت فرق قائل شویم .
سری فیبوناچی چه در ریاضیات چه در فیزیک و علوم طبیعی ، کاربردهای بسیار دیگری دارد ، ارتباط زیبای فاصلههای خوش صدا در موسیقی ، چگونگی تولد یک کهکشان و ... که در مطالب آینده راجع به آنها بحث خواهیم کرد .
این الگو را می توان در گلبرگها یا دانههای بسیاری از گیاهان مثلاً آناناس ، گل داوودی ، گل کلم ، میوههای کاج و ... مشاهده کرد .
خود انسان از ناف به نسبت فی تقسیم میشود . این نسبت نقش پیچیدهای در پدیدههایی مانند ساختار کریستالها ، سالهای نوری فاصله بین سیارات و پریودهای چرخش ضریب شکست نور در شیشه ، ترکیبهای موسیقی ( مبحث هندسه دوجینی و موسیقی ) ، ساختار سیارهها و حیوانات بازی میکند . علم ثابت کرده است که این نسبت به راستی نسبت پایه و مبنای خلقت جهان است . هنرمندان دوره رونسانس عدد فی را یک نسبت الهی میدانستهاند .
از زمانی که هنرمندان و معماران به عمد شروع به استفاده از نسبت طلایی کردند ، نشان داده شد که مخاطبان شیفتگی و شیدایی بیشتری نسبت به کارهای آنها از خود نشان دادند . مستطیلهای طلایی ، مانند نسبت طلایی فوقالعاده ارزشمند هستند . در بین مثالهای بیشمار از وجود این نسبت و یکی از برجستهترین آنها مارپیچ های DNA است . این دو مارپیچ فاصله دقیقی را با هم براساس نسبت طلایی حفظ میکنند و دور یکدیگر میتابند .
در حالی که نسبت طلایی و مستطیل طلایی جلوههای زیبایی را از طبیعت و ساختههای دست انسان به نمایش میگذارد ، جلوه دیگری از این شکوه وجود دارد که زیباییهای تحرک را به نمایش میگذارد . یکی از بزرگترین نمادهایی که میتواند رشد و حرکات کاینات را نشان دهد ، اسپیرال طلایی است .
اسپیرال طلایی که به آن اسپیرال لگاریتمی و اسپیرال متساویالزاویه نیز میگویند هیچ حدی ندارد و شکل ثابتی است . روی هر نقطه از اسپیرال می توان به هر یک از دو سو تا بینهایت حرکت کرد . از یک سو هرگز به مرکز نمیرسیم و از سوی خارجی نیز هرگز به انتها نمیرسیم . هسته اسپیرال لگاریتمی وقتی با میکروسکوپ مشاهده میشود همان منظرهای را دارد که وقتی به اندازه هزاران سال نوری به جلو میرویم . دیوید برگامینی در کتاب ریاضیاتش خاطرنشان میکند که منحنی ستارههای دنبالهدار از خورشید کاملا شبیه به اسپیرال لگاریتمی است . عنکبوت شبکه تارهای خود را به صورت اسپیرال لگاریتمی میبافد . رشد باکتریها دقیقاً براساس رشد منحنی اسپیرال است . هنگامی که سنگهای آسمانی با سطح زمین برخورد میکنند ، مسیری مانند اسپیرال لگاریتمی را طی می کنند . عدد فی Φ عددی مربوط به خلقت پروردگار یکتا است .
اسبهای آبی ، صدف حلزونها ، صدف نرمتنان ، موجهای اقیانوسها ، سرخسها ، شاخهای جانوران و نحوه قرار گرفتن گلبرگهای گل آفتابگردان و چیدمان گل مروارید ، همه به صورت اسپیرال لگاریتمی است . گردباد و منظومهها از نگاه بیرون کاملاً در مسیری به صورت اسپیرال حرکت میکنند . طرح مطالب در این زمینه بسیار بسیار زیاد است که در آینده به آن خواهیم پرداخت .
دنباله اعداد فیبوناچی
دنباله اعداد فیبوناچی
فکر می کنید به چند طریق میتوانید از یک پلکان که دارای n پله است، بالا بروید، در صورتی که در هر گام فقط بتوانید یک یا دو پله را طی کنید؟ برای یافتن پاسخ این مسأله، ابتدا یک حالت ساده را در نظر میگیریم. فرض کنید که پلکان چهار پله دارد. شما میتوانید با چهار گام کوچک ( یک پله ای ) مسیر را طی کنید و یا این که دو گام بزرگ ( دو پله ای ) یا یک گام بلند و دو گام کوچک بردارید. کلیه ی حالت های ممکن در شکل زیر نمایش داده شده است. پله هایی که با علامت مشخص شده اند، پله هایی هستند که روی آن قدم گذاشته اید.
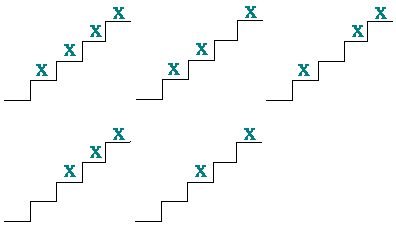
در واقع این مسأله را با یک استراتژی بسیار ساده میتوان حل کرد. کافی است مسأله را کمی کوچک یاساده کنیم. آخرین گام یک گام کوچک یا یک گام بزرگ است. در واقع تعداد راه هایی که میتوان پلکان را طوری طی کرد که به پله ماقبل آخر رسید، حل مسأله برای یک پله کم تر ( n-1 پله ) است و تعداد راه هایی که میتوان از آن به دو پله پایین تر رسید، حل مسأله برای دو پله کم تر ( n-2 پله ) خواهد بود. در مثال بالا سه مسیر مختلف وجود دارد که به پله ی سوم میرسد و دو مسیر وجود دارد که به پله ی دوم منتهی میشود. حال باید مسأله را برای این دو حالت کوچک تر حل کنیم. ما دوباره هر یک از این دو حالت را به حالات کوچک تر مشابه تقسیم میکنیم. این روش را "حل بازگشتی " مینامند. در واقع ما هر بار مسأله را به مسأله ای شبیه خودش - اما کوچک تر از آن - تبدیل میکنیم. تعداد کل مسیرها برابر مجموع مسیرهایی که به پله ی ماقبل آخر رسیده و همین طور مسیرهایی که به دو پله قبل از پله ی آخر منتهی شده اند، میباشد. میتوانید بگویید چرا؟
اگر همین طور مسأله را به مسأله های کوچک تر تقسیم کنیم، در پایان به جایی میرسیم که حل آن برای ما بسیار ساده است: به چند طریق میتوان دو پله را طی کرد؟ و پس از حل آن، دوباره مسیری را که برای حل مسأله طی کرده ایم، باز میگردیم.

| این
مسأله را میتوان با دنباله ی اعداد فیبوناچی نیز حل کرد. دنباله ی
فیبوناچی یک دنباله ی بازگشتی است که در آن اعداد اول و دوم برابر یک
میباشند. هر عدد این دنباله از جمع کردن دو عدد قبلی به دست
میآید. چند عدد ابتدایی این دنباله عبارتند از:.... و 13و 8 و 5 و 3 و 2 و 1 و 1، چون: ...و13=5+8 و 8=3+5 و 5=2+3 و 3=1+2 و 2=1+1
اگر عدد n ام این دنباله را با fn نشان دهیم، آن گاه میتوان دنباله را با فرمول بازگشتی زیر مشخص نمود: fn=fn-1+fn-2 , f1=1 , f2=1 اگر دقت کنید متوجه میشوید که f1 دقیقاً برابر تعداد راه های ممکن برای بالا رفتن از یک پله، f2 برابر راه های ممکن برای دو پله و به همین ترتیب fn تعداد مسیرهای ممکن برای رسیدن به بالای یک پلکان n تایی است. آیا میتوانید توضیح دهید که چرا تساوی بالا برقرار است؟ مسائل بسیاری را میتوان با استفاده از دنباله ی اعداد فیبوناچی حل نمود. این دنباله در سال 1202 میلادی توسط یک ایتالیایی به نام " لئوناردو فیبوناچی " (Leonardo Fibonacci) ابداع شد. در واقع او در جستجوی راه حل یک مسأله بود. مسأله به این صورت است که : " اگر هر جفت خرگوش در هر ماه یک جفت خرگوش جدید به دنیا بیاورند و خرگوش های جدید نیز پس از گذشت یک ماه، به دوران باروری برسند ( با فرض این که هیچ خرگوشی نمیرد )، تعداد خرگوش ها را در ماه n ام به دست آورید. "  | ||
| بعدها،
یوهان کپلر (Johannes Kepler) خاصیت جالب دیگری از این دنباله را
کشف کرد. او نسبت دو جمله ی متوالی این دنباله را محاسبه نمود و متوجه
شد که این نسبت به عدد در مورد عدد طلایی و خواص آن تحقیق کنید . اعداد فیبوناچی را در بسیاری از موارد طبیعی نیز میتوانید مشاهده کنید. آرایش برگها و گل های بسیاری از گیاهان به صورت دو پیچه (spiral) است. معمولاً تعداد پیچه های ساعت گرد با تعداد پیچه های پادساعت گرد تفاوت دارد. این دو عدد در اغلب مواقع دو عدد متوالی از رشته ی فیبوناچی هستند. به شکل زیر توجه کنید:   | ||
| این الگو را میتوان در گل برگها یا دانه های بسیاری از گیاهان مثلاً آناناس، گل داوودی، گل کلم، میوه های کاج و ... مشاهده کرد. شاید دلیل آن این باشد که وقتی دانهها ( یا گل برگها ) به این صورت قرار گیرند، بدون توجه به اندازه ی آن ها به طور یکنواخت و فشرده در کنار هم جای میگیرند؛ یعنی با این که عده ای از دانهها کوچک تر از بقیه هستند، در هیچ ناحیه ای تراکم تغییر نمی کند و فضای خالی دیده نمی شود. | ||
مارپیچ فیبو ناچی
درصورتیکه تعدادی مربع با بُعدهایِ برابر با اعداد فیبوناچی (...،1،1،2،3،5،8) طرح کنید و خطی در راستای قطر هر یک از مربعها رسم کنید، مارپیچ فیبوناچی شکل خواهد گرفت. نمونههای زیادی از مارپیچ فیبوناچی در طبیعت مشاهده میشود، از جمله در ساختار صدف نوتیلوس.

تاریخچه فیبوناچی
0,1,1,2,3,5,8,13,21,34,55,89,144, ...
البته برخی از ریاضی دانان عدد صفر را جزو رشته فیبوناچی نمی دانند و یا حداقل آنرا جمله صفرم سری می دانند. نکته ای که تعجب برانگیز است آنکه اگر از عدد سوم نسبت اعداد این سری را به عدد قبلی حساب کنیم خواهیم داشت :
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
ادامه مطلب ...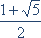 نزدیک میشود. این نسبت، عددی شناخته شده بود که " عدد طلایی " نامیده میشد.
نزدیک میشود. این نسبت، عددی شناخته شده بود که " عدد طلایی " نامیده میشد.